ATB
Simon
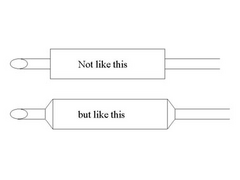
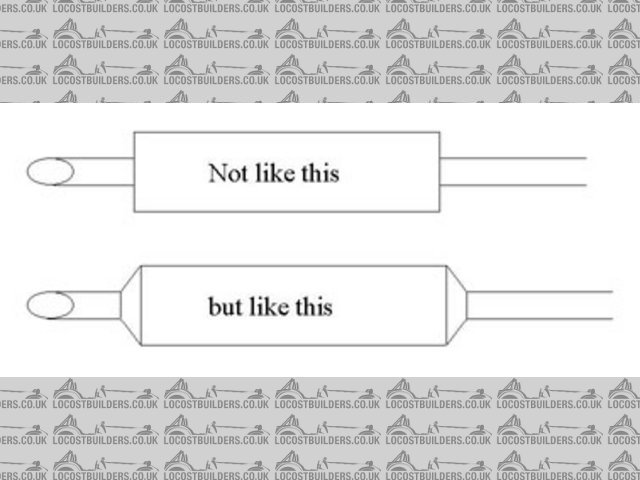
Rescued attachment silencer ends.jpg

Chaps,
Going to make my own silencers, and will need to make some end caps.
Obviously I don't want them "square" but angled (see pic)
Trouble is, I can't remember how to plot out the shape prior to cutting.
5" outer, 2" inner!
Any help much appreciated
Thanks and Regards
Simon
[Edited on 30/12/03 by Simon]
Oops, forgot the pic
ATB
Simon


Rescued attachment silencer ends.jpg
do you mean you want to cut a shape like a C and fold it into a cone?
2" diameter is about 6.3" circumference, so the inner edge wants to be 6.3" round. outer will be about 5pi or 15.5"ish.
the angle of the cone is determined by the size of the initial flat circle.
if you used the full 360 degrees of the initial circle, rather than with a bit missing to make it C shaped, then obviously the cone will be flat. if
you use 180 degrees, keeping the sizes 6.3 and 15.5 by making the circle bigger, then the angle will be steeper.
unfortunately i cant think how to choose an angle and make a cutout of the right size. might come to me soon though...!
edit:
if you know the bottom of the cone wants to have a radius of 2.5 inches, then pick a prefered angle, and work out the length of a slope to a peak
(imagine it will be a full cone at first). this is easiest by pythagoras if you pick 45 degrees, otherwise you need cos etc...
the length if the side of the cone is the radius of the outer circle when the cutout is flat. you work out the number of degrees of the circle you
want by comparing the cone circumference (5 pi) to the flat circle circumference.
then work out the size of the inner circle to remove, by a similar way.
hope that helps anyway!
[Edited on 30/12/03 by JoelP]
thats complicated shit, you have your 2 radii and can calculated the length and angle of the slope easy enough but when flat ie when you mark it out
on sheet metal) the radii will change.
i would make a wooden former and shape the metal around that, itll be much easier to get the shape you want and keep it that way.
Russ.
edited my post a bit...
quote:
Originally posted by suparuss
you have your 2 radii and can calculated the length and angle of the slope easy enough
Russ.

Chaps,
Thanks for your efforts - I'm going to make cone from paper or something, then mark and cut the the inner and outer radii, at the correct
angle/dimensions, then transfer to sheet steel.
Another route would be to make a 5" disc, weld on a piece of 2" tube (length determined by angle I want), then go over edges with marker
pen/felt tip/grease etc, and roll it over the paper. That'll trace out the shape req'd.
Thanks again.
ATB
Simon
Jeyes Fluid! Way too hard! Just take your drawing to a metal spinner and they'll knock out some end caps for less than you can buy the materials for...no welds, smooth, and polished.
If Simon lived in the Midlands, Brimingham area, or similar, then a metal spinner would be ideal...
...but the chances of finding a metal spinner in Tunbridge Wells (or Ipswich, for that matter) are remote! 
It is the ideal solution, though.
rgds,
David
Conic sections
Not as hard as you would think at first glance.
I don't know how to include drawings here so I hope I can explain it well enough, refer to Simon's drawing of the silencer with
'angled' ends.
Try this on paper first.
Draw a line the diameter of the silencer and label the ends A & B
Draw two further lines from points A & B at the required angle of the cone, these should intersect to form an equalateral triangle, label the
intersection C
Draw a line parrallel to A,B the same length as the diameter of the outlet / inlet pipe so as it touches lines A,C and B,C. Label the ends of this
line D & E.
On a fresh area of the paper draw a circle with a radius equal to the length of line A,C
Using the same centre draw another circle of radius equal to the length of line C,D
You should have drawn a doughnut shape.
Using the compass step three times the length of A,B around the circumfrence of the large circle.
Join the first and last points to the centre of the circle, (forming two radii).
Cut out the doughnut and cut along the two radii
You now have two sections of doghnut. Take the one which you stepped out with the compass and bend it until the two radii meet.
You should be holding a truncated cone section with holes of diameter equal to A,B and D,E
Hope this makes sense, try it it's dead easy whern you've done it once.
Mick
[Edited on 31/12/03 by Mix]