[Edited on 1/11/2010 by mcerd1]

... going on from my socket screw question, I want to get a feel, literaly, on how much force it would take to sheer one of these socket screws.
So the question is, how do I calculate the force produced by a screw of known pitch when I apply a known force to turn it.
i.e. force produced by a vice.
I can measure force via scales and lever length and can work out the pitch of the lead screw.
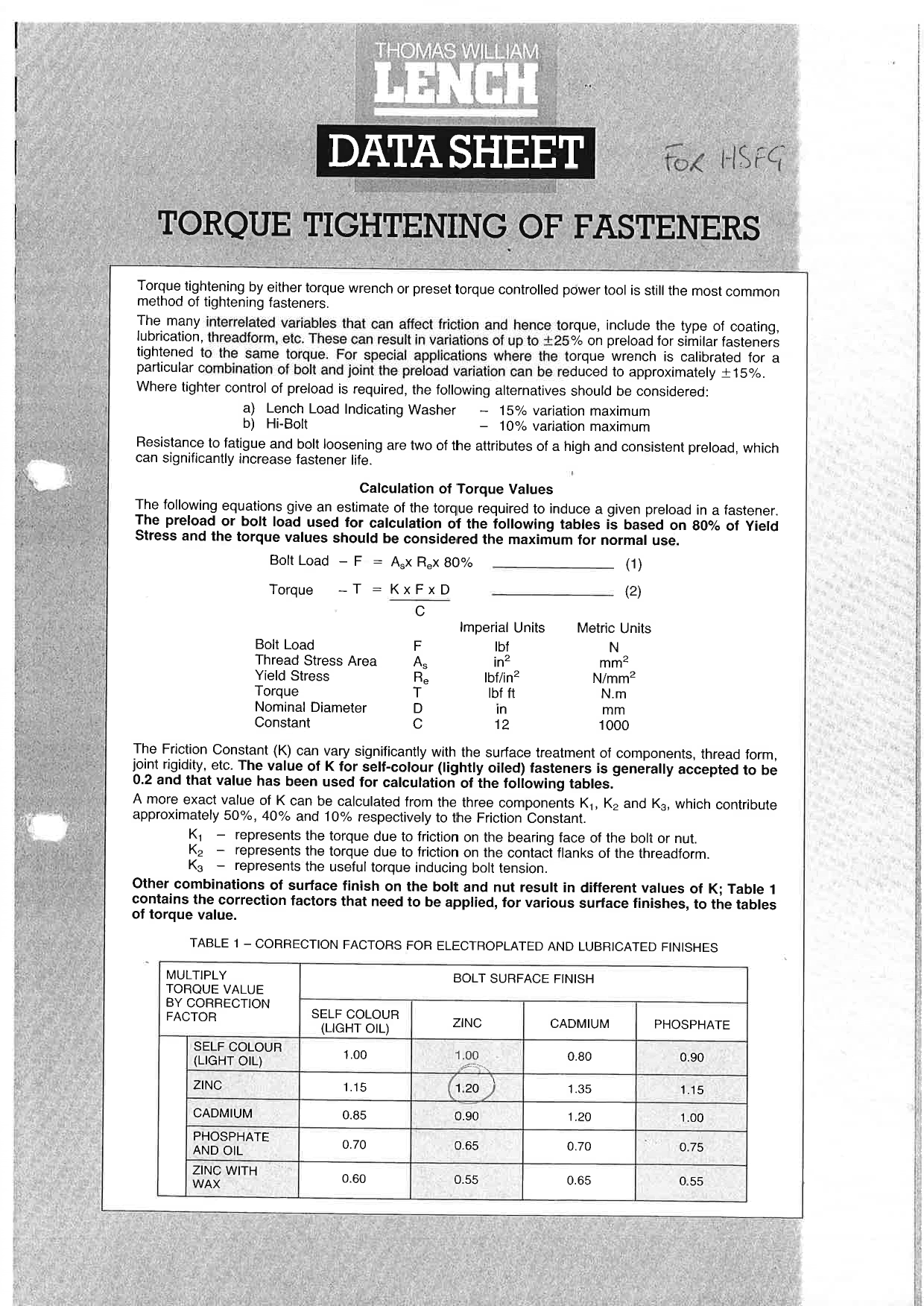
This might help you.
However, in the real world it's often not possible to calculate the relationship between fastener torque and clamping load to a useful accuracy
since so much of the torque go into overcoming friction in the threads and between the fastener and the item being clamped. This friction depends on
the fastener material, quality of finish, presence of lubrication etc. This is why critical fasteners often use angular torque settings.
[Edited on 1/11/10 by MikeRJ]
I am a physicist, so as a rule ignore friction.
Force * distance = work
So force on the end of the lever*distance around
will equal the force on the vice * the distance moved.
You can also do
Force * velocity = rate of work (which is also constant).
No-one really understands friction, so I ignore it (unless I'm on my bicycle).
Matt
Torque applied to a bolt essentially stretches the bolt and the clamping force is proportional to the amount of stretch.
For example the recommended torque figures for bolts take them to 70% of their yeild strength, and therefore produce a certain amount of stretch in
the bolt. You can them work out how much force is requires to stretch the bolt that amount and that is the amount of clamping force applied.
Basically you can work it out if you know the Youngs Modulus of the material, and how much stretch there is on the bolt.
However in reality its a lot more complicated that that.
You can approximate the tension in a bolt with:
T = Fp * K * d
Where T is torque (Nm), Fp is Bolt tension (Newtons), K is a constant (.2-.3 for steel bolts) and d is diameter (m) which would get you somewhere
close.
So an M4 bolt tightened to 20Nm would give you a bolt tension, and therefore clamping force of approx 16500N or 1690Kg. But like I say its only
approximate and in reality a lot more complex
That probably doesnt make sense....
[Edited on 1/11/10 by flak monkey]
maybe this will help explain it:

[Edited on 1/11/2010 by mcerd1]
quote:
Originally posted by matt_gsxr
I am a physicist, so as a rule ignore friction.constant).
No-one really understands friction, so I ignore it (unless I'm on my bicycle).
Matt

quote:
No-one really understands friction, so I ignore it (unless I'm on my bicycle).
ooops, I should have said there is no clamping force on the socket screw; so it is just sheering the 5 mm socket screw.
question boils down to how twisting force translates to linear force.
[Edited on 1/11/10 by 02GF74]
quote:
Originally posted by Bluemoon
quote:
No-one really understands friction, so I ignore it (unless I'm on my bicycle).
If you do that you will snap fasteners, or under torque them see above table.. That's the problem the actual values can only be found by experiment (I am also an experimental physicist, and this is when a first-order approximation is just not good enough).
Dan
[Edited on 1/11/10 by Bluemoon]
quote:
Originally posted by 02GF74
question boils down to how twisting force translates to linear force.
http://www.roymech.co.uk/Useful_Tables/Form/Stress_Strain.html
quote:
Originally posted by flak monkey
quote:
Originally posted by 02GF74
question boils down to how twisting force translates to linear force.
It doesnt, you work in shear stress instead.
ok
first you need to work out the shear force needed to shear the bolt - so grade of M5 bolt are you takling about ? (most cap heads are 12.9)
then you'd need to know the properties of the vice thread and the friction involved (alot of good vices will have a different type of thread to
bolts - these have lower friction so more of torque will end up doing what you want it to)
that is all in theory at least - most bolts should be a little better than there design strength
in reality it would be easier to get a torque gauge and see what it takes.....
^^^^ I don't to calculate sheer force.
I want to know if I apply 10 kg on a 1 ft vivc lever, how much force do the jaws apply ... and I will up the force until the socket screw pops. The
properties of the socket screw don't come into it ... or do they?
maybe it is not that simple......
the bolt properties will tell you how much you'll need to put into it to snap the bolt 
it you just want to know how much force the jaws apply you could:
- stick a spring of a know rate in the jaws (like one of you car which will have a rate in lb's/inch or N/mm)
- then see how much it squashes with your 10 ft.kg's (or ~22ft.lbs in real units)
[Edited on 1/11/2010 by mcerd1]
It's not that simple. I think.
You can say (ignoring the screw distorting) that X degrees of screw rotation will advance the end of the screw Y mm depending on the thread pitch. How
much force is required to distort the material the screw is pushing against is dependent on how hard that material is. The amount of torque you need
to apply to the screw to make it turn that amount is therefore going to be dependent on the hardness of that material, friction between the end of the
screw and the compressed thingy, friction in the threads.
This may possibly be utter codswallop, I'm normally an electron herder 
Work out the shear strength of the bolt (see my last post on your similar thread) This will tell you how much load you need to apply to the bolt to
shear it.
Then use the calculation above to work out what torque you need to apply to the vice handle. In order to calculate it you need to know the diameter of
the screw in the vice.
Its only a rough approximation, but would get you close.
So for example - say the shear strength of the bolt is 20,000N (its too late to work out what it really is) so you would need to apply that amount of
force to shear it off.
Assume the vice has a 20mm (0.02m) screw to provide the clamping force and its steel on steel so use a .25 coefficient.
The Torque required would be:
20,000*.25*.02 = 100Nm
This doesnt take into account a lot of factors such as friction on the 2 sliding tubes and deformation of various bits (assumes the vice is totally
rigid for a start).
Other than that, it seems like a reasonable approximation.
Oh it also assumes you are shearing the bolt at the point which it exits the inside diameter of the tube it is radially screwed through.
if you have a copy, the bosch automotive handbook (its a bible by the way) has pretty good information on fastener torque calculation incorporating
assumed friction values for various greases, finishes etc etc
I used it a while back for Lobro joint bolt torques and they seemed pretty much spot on (forget the exact maths, but I deliberately then overtorqued
one to shear it and it was about bang on predicted for that class fastener's strength)
Think of it like a lever.
If you had a lever the 'force multiplier' is the ratio of how far your hand on the lever moves compared to how far the object moves - e.g if
your force is aplied at 10cm from the pivot, and the thing you want to lift is 1cm from the pivot, the force on the object is 10 times higher. For the
screw as a vice example, if your lever was 10 cm long, in one rotation your hand moves 314mm. On a 1mm pitch screw, this gives a movement ratio of 314
to 1, e.g a 1kg weight on the end of the lever will pull the vice jaws together with a force of 314kg. Obviously you cannot exceed the yield strength
of the screw or it will stretch or break, or the yield strength of the engaged thread (depends on thread depth and yield strenth of screw and nut) or
it will strip the thread. Remember to grease the threads to reduce friction.
Regards
Hugh