
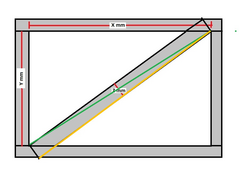
OK, so the rectangle dimensions X and Y are known, and the width of the tube Z is known, but I cannot see to get calculate the actual length and angle (if I knew one I could work out the other)
Anyone help?

I'm trying to work out how to calculate the length and angles of a diagonal in a rectangulat aperture, done as shown in the picture

OK, so the rectangle dimensions X and Y are known, and the width of the tube Z is known, but I cannot see to get calculate the actual length and angle
(if I knew one I could work out the other)
Anyone help?
Someody should have taken more notice during geometry classes at school!
And your drawing isnt clear!
Seriously, lets see if i can explain how to find this while also simplifiying your drawing!
The easiest way is to ignore the thickness of the tube for now (as thats where you have one problem), lets treat it as a simple triangle.
X is the length of your horizontal (but it stops 25mm to the left of where you have drawn it)
Y is the length of the upright
Z is the length of your diagonal
Z(squared) = X(squared) + Y(squared)
Z = the square root of { X(squared) + Y(squared) }
Any scientific calculator will have the symbols for the functions, shame a qwerty keyboards doesnt.
Hope this helps
If that design is for a bulkhead the cross piece in wrong.
quote:
Originally posted by slingshot2000
Someody should have taken more notice during geometry classes at school!
And your drawing isnt clear!
Seriously, lets see if i can explain how to find this while also simplifiying your drawing!
The easiest way is to ignore the thickness of the tube for now (as thats where you have one problem), lets treat it as a simple triangle.
X is the length of your horizontal (but it stops 25mm to the left of where you have drawn it)
Y is the length of the upright
Z is the length of your diagonal
Z(squared) = X(squared) + Y(squared)
Z = the square root of { X(squared) + Y(squared) }
Any scientific calculator will have the symbols for the functions, shame a qwerty keyboards doesnt.
Hope this helps
quote:
Originally posted by designer
If that design is for a bulkhead the cross piece in wrong.
Length of diagonal from corner to opposite corner = sqrt(X^2 + Y^2)
Call the maximum length of the diagonal before the sloped cuts are made D.
sqrt(X^2 + Y^2) = sqrt(D^2 + Z^2)
Therefore, D = sqrt(X^2 + Y^2 - Z^2).
I think.
quote:
Originally posted by BenTyreman
Length of diagonal from corner to opposite corner = sqrt(X^2 + Y^2)
Call the maximum length of the diagonal before the sloped cuts are made D.
sqrt(X^2 + Y^2) = sqrt(D^2 + Z^2)
Therefore, D = sqrt(X^2 + Y^2 - Z^2).
I think.
It's not a simple pythagorean equation because of the width of the tube..... Personally I'd just draw it up in CAD and measure the mofo 
quote:
Originally posted by interestedparty
I'm not quite seeing that. D has already been found (pythagoras) from X and Y which are known, yet your last formula shows it as a variable, because X, Y and Z are already known.
quote:
Originally posted by BenTyreman
quote:
Originally posted by interestedparty
I'm not quite seeing that. D has already been found (pythagoras) from X and Y which are known, yet your last formula shows it as a variable, because X, Y and Z are already known.
What I call D is the length of the diagonal if it were to be cut square as short as possible, i.e. the minimum length possible before the sloping cuts are made.
Pythag. of X and Y gives a distance that crosses the width of the diagonal member. The extra step accounts for the width of the diagonal tube.

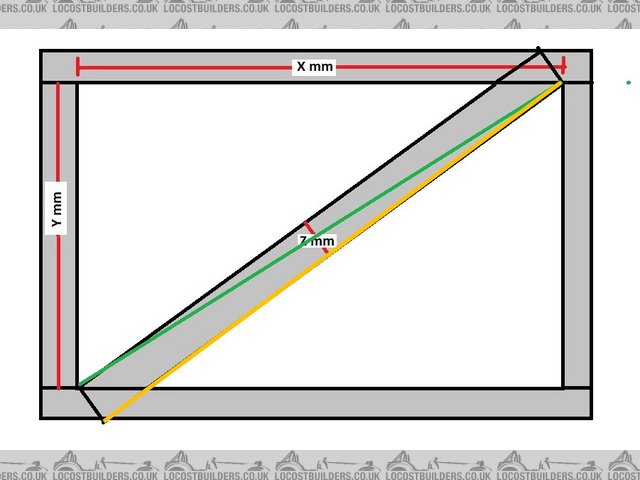
Description
Green line = sqrt(X^2 + Y^2)
Green line = sqrt([Yellow line]^2 + Z^2) = sqrt(X^2 + Y^2)
[Yellow line]^2 + Z^2 = X^2 + Y^2
[Yellow line]^2 = X^2 + Y^2 - Z^2
Yellow line = sqrt(X^2 + Y^2 - Z^2)
So if the green line here is D (and I've sketched in the full tube), can you axplain how your formula works, as I'm still not getting it.
Thanks for your efforts, BTW.

Thanks chaps, I think I've ot enough to be going on with. Just need to digest this and work out the best way to proceed.
I'd still be interested in getting an answer to the "If that design is for a bulkhead the cross piece in wrong" point that was made.
If you are hoping to use that diagonal to brace a bulkhead, (or any other rectangle), the centre line of the digonal tube really wants to extend
through the external corners of the rectangle.
IE; both ends of the diagonal should be exacly the same and be an 'arrow-head', same chamfeur on each side @ each end.
All the three centre lines must meet at the same point.
Take the centre line of the top and side pieces and the centre line of the diagonal must meet at the same point.
My head hurts reading this! 
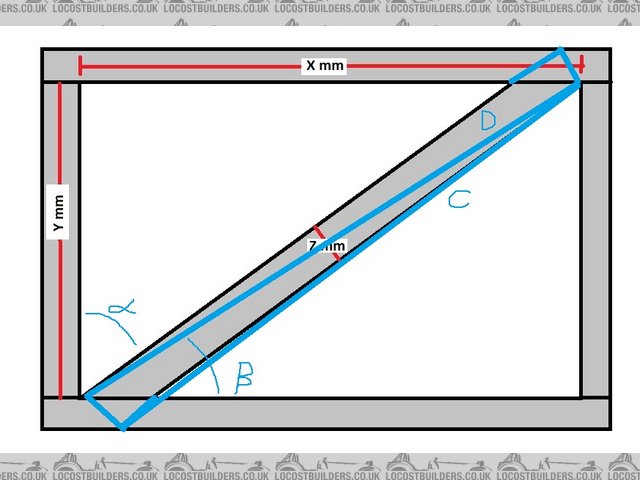
Simples really.
Line D is simple pythagorous.
D is just the diagonal of tube length C, width Z.
This gives us C.
The angle between C and D can now be found through trig as can beta.
Alpha is 90 minus those two angles combined.
cos alpha = Y / [length of tube minus cut off bit]. This then gives the length of the side of the parallelogram and therefore also the amount you need
to chop off.
The length of the off-cut plus the tube thickness can then be used to work out the angle between the off-cut and the horizontal bar X.