Gav
|
| posted on 18/11/06 at 07:32 PM |

|
|
Anyone good at Maths?
Would i be right in saying that
1/3(x+2)^2-12 = 2/3x^2+2x-12 ?
[Edited on 18/11/06 by Gav]
|
|
|
|
|
JoelP
|
| posted on 18/11/06 at 07:37 PM |

|
|
do you mean:
(1 / (3(x+2))) squared
or
(1/3 (x+2)) squared?
first is equal to 1/(3x+6) squared which surely is 1/(9x^2+36) edit, actually 1/(9x^2+36x+36)
second is (x^2+2x+4)/9
unless ive forgotten how to square fractions.  
thats obviously ignoring the -12, which is the same on both sides.
[Edited on 18/11/06 by JoelP]
[Edited on 18/11/06 by JoelP]
|
|
|
DIY Si
|
| posted on 18/11/06 at 07:41 PM |

|
|
Don't think so.
Any way you could write out what you mean and show it on here? It would be much easier to understand that way.
[Edited on 18/11/06 by DIY Si]
“Let your plans be dark and as impenetratable as night, and when you move, fall like a thunderbolt.”
Sun Tzu, The Art of War
My new blog: http://spritecave.blogspot.co.uk/
|
|
|
matt.c
|
| posted on 18/11/06 at 07:46 PM |

|
|
What the?  
lost me big time!

|
|
|
Gav
|
| posted on 18/11/06 at 07:50 PM |

|
|
ok i need to get 1third times (x+2) squared - 12 into a quadratic ie ax squared + bx + c
[Edited on 18/11/06 by Gav]
|
|
|
arrybradbury
|
| posted on 18/11/06 at 07:51 PM |

|
|
The straight answer is no (i think):
Thought as:
(x+2) squared multiplied by 1/3 and then subracting 12 gives:
(1/3 * (x^2 + 4x + 4)) - 12
= (1/3 * (x^2 + 4x + 4)) - 36/3
= 1/3 * (x^2 + 4x - 32).....
any help??
|
|
|
DIY Si
|
| posted on 18/11/06 at 07:54 PM |

|
|
easiest way to show it, without lots of fractions in it is 1/3 * (x^2 + 4x - 32 )
“Let your plans be dark and as impenetratable as night, and when you move, fall like a thunderbolt.”
Sun Tzu, The Art of War
My new blog: http://spritecave.blogspot.co.uk/
|
|
|
JoelP
|
| posted on 18/11/06 at 07:54 PM |

|
|
1/3 * (x+2)^2 - 12
1/3 * (x^2+4x+4) - 12
1/3x^2 + 4/3x + (4/3 -12)
1/3 x^2 + 4x/3 - 32/3
3 answers and we all agree! 
[Edited on 18/11/06 by JoelP]
|
|
|
DIY Si
|
| posted on 18/11/06 at 07:55 PM |

|
|
Or as an open thing 1/3x^2 + 4/3x -32/3
“Let your plans be dark and as impenetratable as night, and when you move, fall like a thunderbolt.”
Sun Tzu, The Art of War
My new blog: http://spritecave.blogspot.co.uk/
|
|
|
JoelP
|
| posted on 18/11/06 at 07:56 PM |

|
|
i edited mine due to the confusion over 4/3x and 4x/3, technically the same thing but it can be read wrong! 
|
|
|
Gav
|
| posted on 18/11/06 at 07:56 PM |

|
|
just eating my tea, ill give a smartie point to the correct answer, ill work it if its right for my parabola after tea 
|
|
|
DIY Si
|
| posted on 18/11/06 at 07:57 PM |

|
|
True, that's why I put it the first way first. Leaves less to the imagination.
“Let your plans be dark and as impenetratable as night, and when you move, fall like a thunderbolt.”
Sun Tzu, The Art of War
My new blog: http://spritecave.blogspot.co.uk/
|
|
|
DIY Si
|
| posted on 18/11/06 at 07:58 PM |

|
|
If you can post a graph of the parabola with a few important point son it, we can probably get you the answer before you've finished your tea.
“Let your plans be dark and as impenetratable as night, and when you move, fall like a thunderbolt.”
Sun Tzu, The Art of War
My new blog: http://spritecave.blogspot.co.uk/
|
|
|
owelly
|
| posted on 18/11/06 at 08:02 PM |

|
|
Is the correct answer 2 hats?
http://www.ppcmag.co.uk
|
|
|
Gav
|
| posted on 18/11/06 at 08:14 PM |

|
|
parabola:
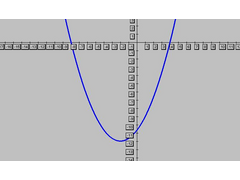 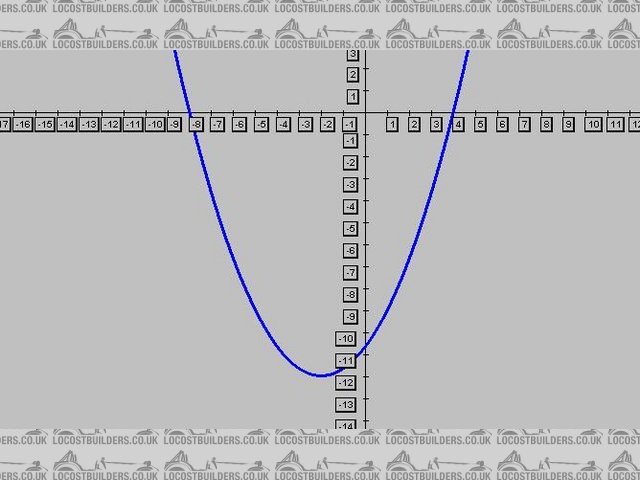
Description
ok the problem i have is that when i converted the equation 1/3(x+2)^2 - 12 to a quadratic i found the to x-intercepts to be 4.3 and -9.7 which is
close but obvisouly not right!
edit: yes im trying to prove the x-intercepts are correct.
[Edited on 18/11/06 by Gav]
|
|
|
clanger
|
| posted on 18/11/06 at 08:15 PM |

|
|
too long ago without a trip to the attic, but my attempt
x^2+4x-6 ..............??????
car building and maths questions...wot a site 
|
|
|
DIY Si
|
| posted on 18/11/06 at 08:20 PM |

|
|
does it bottom out at -12, -2?
“Let your plans be dark and as impenetratable as night, and when you move, fall like a thunderbolt.”
Sun Tzu, The Art of War
My new blog: http://spritecave.blogspot.co.uk/
|
|
|
Gav
|
| posted on 18/11/06 at 08:25 PM |

|
|
The vertex is correct at -2, -12
Just found another example which is correct:
-2(x-1)^2 + 1 = -2x^2 + 4x -1
its factorising i suck at, especially when fractions are involved :S
|
|
|
DIY Si
|
| posted on 18/11/06 at 08:29 PM |

|
|
The equation is, I think, 1/3 x^2 + 4/3 x - 32/3
Or, 1/3 * ((x +8)(x -4))
[Edited on 18/11/06 by DIY Si]
“Let your plans be dark and as impenetratable as night, and when you move, fall like a thunderbolt.”
Sun Tzu, The Art of War
My new blog: http://spritecave.blogspot.co.uk/
|
|
|
Gav
|
| posted on 18/11/06 at 09:13 PM |

|
|
You were close but not quite right 
Answer is 1/3x^2 + 4/3x - 12
which gives -8.234 and 4.324 which if you look at the parabola looks just about right for the x-intercepts
|
|
|
DIY Si
|
| posted on 18/11/06 at 09:16 PM |

|
|
can't be -12, or it would cross the y axis at -12!  Instead it crosses at -10 2/3. Instead it crosses at -10 2/3.
Besides even if i am wrong (and it's been known to happen ), it's the first bit of algebra I've done since A levels, which was 4
years ago. ), it's the first bit of algebra I've done since A levels, which was 4
years ago.
[Edited on 18/11/06 by DIY Si]
“Let your plans be dark and as impenetratable as night, and when you move, fall like a thunderbolt.”
Sun Tzu, The Art of War
My new blog: http://spritecave.blogspot.co.uk/
|
|
|
Gav
|
| posted on 18/11/06 at 09:21 PM |

|
|
Actually you are right
Answer is 1/3x^2 + 4/3x - 32/3 which gives -8, 4
Which was first seen on the first page by joel 
|
|
|
DIY Si
|
| posted on 18/11/06 at 09:24 PM |

|
|
                  
Also why I put it in the form above, as it makes finding the crosses easy, as you just have to make either bracket equal 0 to find the two, ie -8 for
the first bracket and 4 for the second.
[Edited on 18/11/06 by DIY Si]
“Let your plans be dark and as impenetratable as night, and when you move, fall like a thunderbolt.”
Sun Tzu, The Art of War
My new blog: http://spritecave.blogspot.co.uk/
|
|
|
Gav
|
| posted on 18/11/06 at 09:27 PM |

|
|
a well at least ill sleep well tonight after ive finished this bottle or brandy to cure the headache this gave me 
[Edited on 18/11/06 by Gav]
|
|
|
Gav
|
| posted on 18/11/06 at 09:32 PM |

|
|
Forgot to say, thanks for the help chaps 
|
|
|